Data Structures for Games: Priority Queue for Unity in C#

One of my professors used to say that applications are nothing but data structures and algorithms together. I don’t know if this theory still holds, but data structures are quite important parts of any kind of application including games.

At the time of writing this post Priority Queue wasn’t part of the Collections library but it is now under the System.Collections.Generic.PriorityQueue, This is introduced with .NET 6 . So I’d like to reframe this post as “why a Priority Queue is useful and how it works internally?”

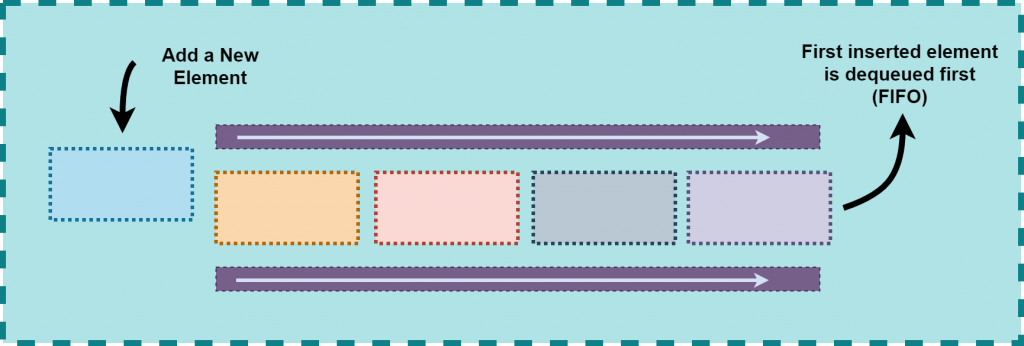
Priority Queue is a special type of a Queue. Whereas a standard Queue works on first in, first out (FIFO) principle, a priority queue works with priorities assigned to each item. High priority items are dequeued before the elements with low priority.

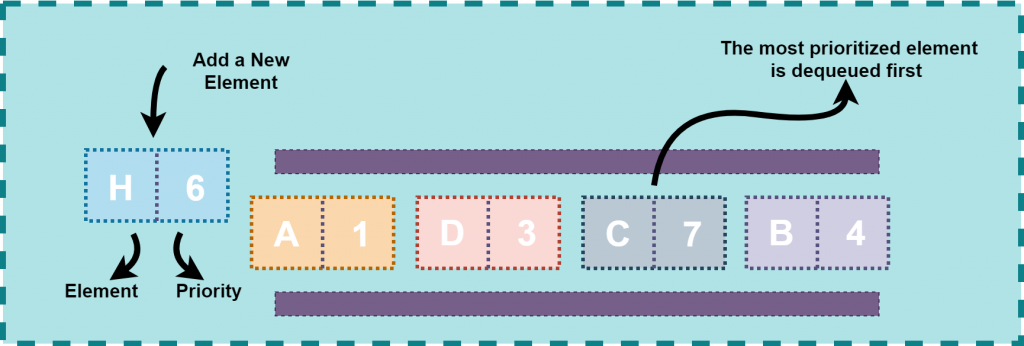
Applications of Priority Queue

Before going in details of Priority Queue, let’s see in which cases we can use it.

I have mostly used a priority queue for solving AI problems in my games. Let’s say we are creating a cool bot for a board game. This game provides you three moves at each turn. The bot will decide which order of the moves are the most valuable ones for the next turn.

As a simple solution to this AI problem, we can have a tree structure. The root represents the current state of the board. It will have many children representing the three moves to the available positions (in my game, it was around 270 children). Then, at every child we will have other possible moves to the available positions. At the end, we will evaluate the value of each chain of moves in the leaves of this tree.

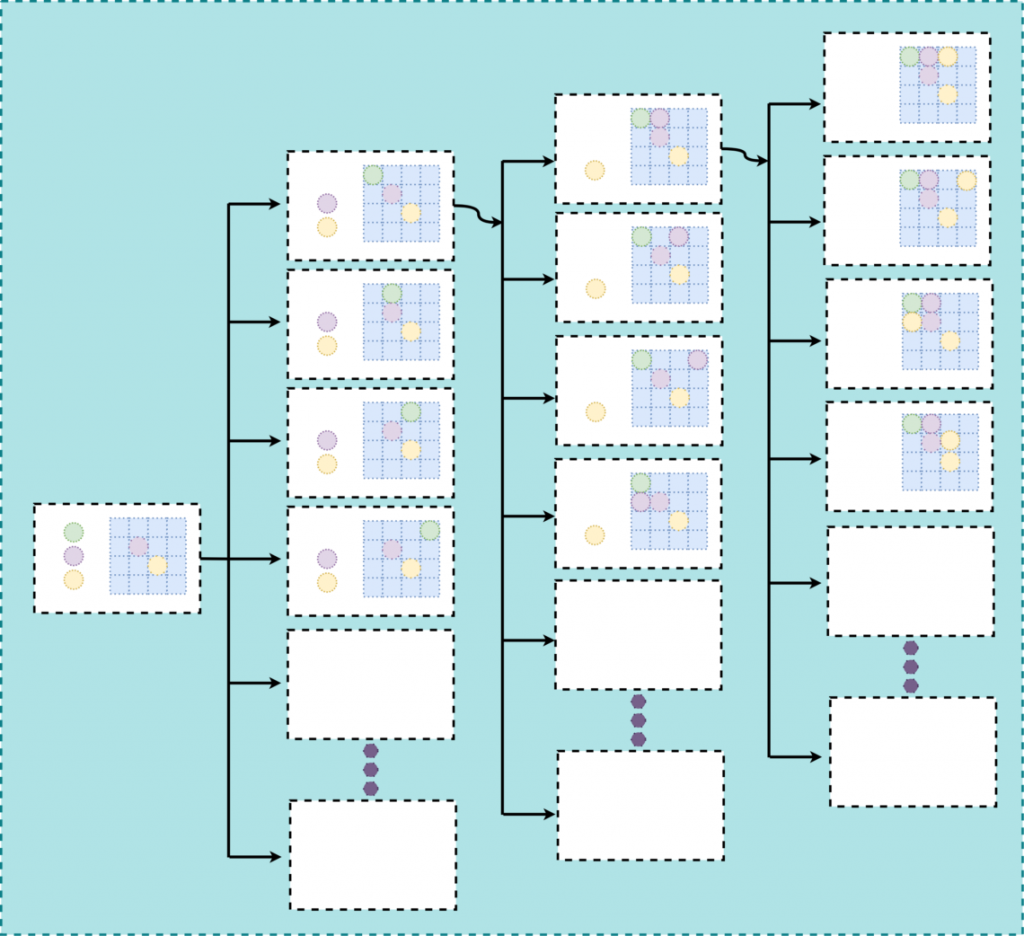
I could keep some kind of score property in the nodes, then sort the leaves of the tree, based on the score. Then I could pick the highest one. However, I preferred to use a Priority Queue. So, I have placed the nodes with their score as a priority. Why?

• It helped me to optimize this query. Instead of evaluating 270 children, I have traversed only the most prominent ones.
• In order to create different levels of difficulty. Based on the chosen difficulty, priority queue gave me the second best or the third best set of prominent children.
• I have also wanted to hide sorting and choosing best candidate behaviors from the evaluation of the tree. It was already quite complex and I didn’t want it to be more complex.
• It was reusable for other bot implementations.

So I am quite happy with the results.

Other possible usages of Priority Queues

• Dijkstra’s Shortest Path Algorithm can be implemented using Priority Queue.
• It can be also used to implement Huffman’s compression algorithm.
• A* path finding algorithm
• A sorting algorithm called Heap Sort is implemented using Priority Queue
• It is possible to give more examples like Prim’s algorithm, or Load
• Balancing algorithms. Simply, we can use it everywhere that is an application of queue where priority is involved.

So, How to Implement a Priority Queue?

As I’ve stated before, Priority Queue is part of the Collections library after .NET 6.

If you would like to implement it yourself, then you can follow up further from here.

Well, let’s know our requirements first;

• We need items with priorities.
• These items will be inserted into somewhere, a container or a list.
• We should be able to reach or delete the element with the highest
  priority.

public interface IPriorityQueue<T>
{
    /// Inserts and item with a priority
    void Insert(T item, int priority);

    /// Returns the element with the highest priority
    T Top();

    /// Deletes and returns the element with the highest priority
    T Pop();
}

We can obviously have more features but let’s keep it simple.

Items with Priorities

I guess, this is easy. We can just have a struct with two fields.

struct Item
{
    int element;
    int priority;
}

Insert

In order to support insert operation we can use a List. It will take only O(1) time, so it is not bad.

Top() and Pop()

Using List structure was good for Insert method, but for Top() and Pop() methods, it may not be the best. Because we need to sort the list based on the priorities, then pick the first or the last element based on the sorting order.

If we use a Linked List, it would take less time for Pop(). However, I believe that our most important method here is the Top(). Therefore, we should be looking for optimizing it.

What About Using Heaps?

When it comes to Priority Queue implementation, Heaps are the best candidate. It provides much better performance then lists. Only drawback is the Insert performance (It would be O(log n)) which is not
a big loss. Pop() can be done in O(log n) and most importantly Top() will be in O(1) time. As far as I know, current C# implementation is using min-heap.

A Binary Heap is a binary tree that satisfies the heap property. For a min-heap, the value of each node is greater than or equal to the value of its parent, meaning the root always holds the minimum value. A max-heap is the opposite. Operations like insert or delete must always maintain this property.

There are also more relaxed heap structures. A Fibonacci Heap is a good example that has a better amortized complexity due to its flexible nature. It does its work lazily, so most operations are O(1) on average.

Back to the Priority Queue

Since we will implement the Priority Queue using Fibonacci Heaps, we should be aware of that, it maintains a min-heap property. Therefore, the priority being represented by a lower number, would have a higher priority. For instance, let’s think a set like {1, 4, 3, 5}. The highest priority will be ‘1’ in this set.

public class PriorityQueue<TElement, TPriority> : IPriorityQueue<TElement, TPriority> 
where TPriority : IComparable<TPriority>
{
    private readonly FibonacciHeap<TElement, TPriority> heap;

    public PriorityQueue(TPriority minPriority)
    {
        heap = new FibonacciHeap<TElement, TPriority>(minPriority);
    }

    public void Insert(TElement item, TPriority priority)
    {
        heap.Insert(new FibonacciHeapNode<TElement, TPriority>(item, priority));
    }

    public TElement Top()
    {
        return heap.Min().Data;
    }

    public TElement Pop()
    {
        return heap.RemoveMin().Data;
    }
}

As you see in the above implementation, it is just so easy to implement a priority queue backed with a Fibonacci heap. The full code is here, however it is written quite a long time before, so please use it for learning purposes.

Priority Queue in Modern C# & Unity

The great news is that you no longer have to build this yourself! Since .NET 6, C# has a built-in PriorityQueue<TElement, TPriority> class available in System.Collections.Generic. Modern versions of Unity (using .NET Standard 2.1 and above) support this. So, please prefer this solution unless you do really have a custom requirement.

It’s implemented as a min-heap, which means lower priority numbers are considered higher priority. For instance, in a set of priorities {1, 4, 3, 5}, the item with priority 1 will be dequeued first.

Here is how simple it is to use:

using System;
using System.Collections.Generic;

public class PriorityQueueExample
{
    public void Run()
    {
        // The queue stores strings (TElement) with int priorities (TPriority)
        var pq = new PriorityQueue<string, int>();

        pq.Enqueue("Low Priority Task", 5);
        pq.Enqueue("High Priority Task", 1);
        pq.Enqueue("Medium Priority Task", 3);

        // Dequeue will return "High Priority Task" first 
        string highestPriorityItem = pq.Dequeue(); // "High Priority Task"

        Console.WriteLine(highestPriorityItem);
    }
}

What If I’m on an Older Unity Version or Need a Custom Implementation?

If you can’t use the built-in class, my original advice still stands: find a good, heap-based library. The repository I created for this article is still available and can be a good learning resource.

Conclusion

A priority queue can be incredibly useful, especially when your game requires some kind of decision-making process. It can hide unnecessary complexity and be very performant.

While the C# Collection API now contains this data structure out of the box, understanding why it’s built on a heap and when to use it is knowledge that will always be valuable. I am planning to maintain my Data Structures repository with new posts. If you have questions, please drop me a comment below.

Feel free to contribute to the repository as well! (Please use the development branch for pull requests).